Más ejemplos de backtrack

Introducción

A continuación veremos otros ejemplos de backtracking aplicado para encontrar distintas soluciones a problemas de gráficas. Incluiremos una representación visual de los resultados obtenidos.

Generar caminos en una gráfica

Encontrar todos los caminos de \(u\) a \(v\) en una gráfica. Ahora los potenciales candidatos son vértices que no hayan sido visitados con anterioridad. Sí nos importa el orden.

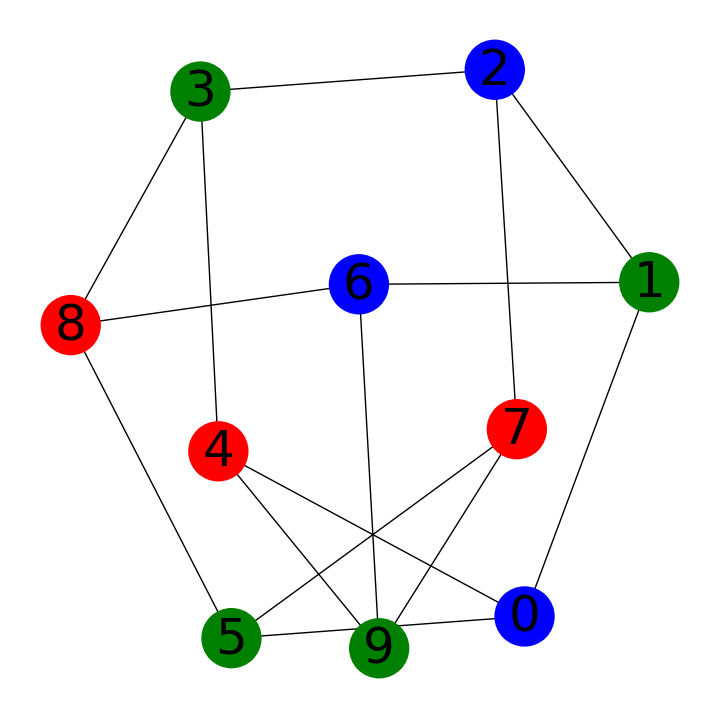
Abajo representamos a la gráfica de Petersen con sus respectivos vértices y aristas.

import networkx as nx

G=nx.petersen_graph()

print(nx.nodes(G))
print(nx.edges(G))
nx.draw(G,with_labels=True)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[(0, 1), (0, 4), (0, 5), (1, 2), (1, 6), (2, 3), (2, 7), (3, 4), (3, 8), (4, 9), (5, 7), (5, 8), (6, 8), (6, 9), (7, 9)]

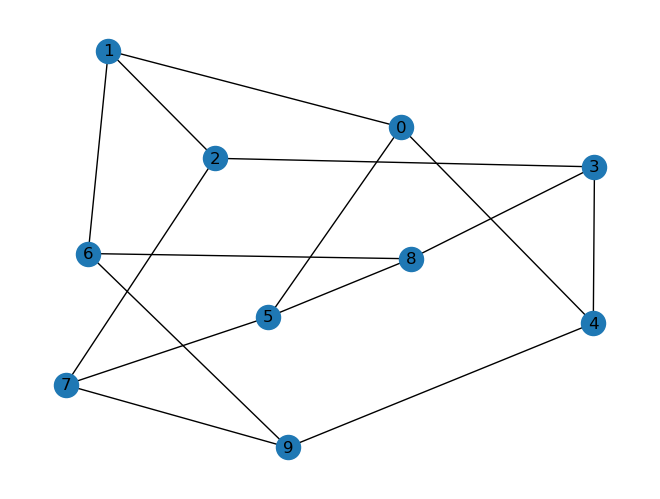
¿Cuántos caminos hay de \(0\) a \(6\)? Los hacemos mediante backtrack.

Armamos caminos empezando por el vértice inicial, que es \(0\). Luego, para elegir el siguiente vértice en un camino, tomamos el último vértice visitado e incluimos alguno de los vértices candidatos entre sus vecinos. Las soluciones válidas serán todos aquellos caminos que terminan en el vértice final, que es \(6\).

def paths(G,u,v,a=[],sols=[]):
    if len(a)==0:
        a.append(u)
    if a[-1]==v:
        sols+=[a.copy()]
        return sols
    candidates=[]
    # Aquí abajo hay algo cuadrático sucediendo que se puede mejorar pasando candidates en la recursión
    for j in nx.all_neighbors(G,a[-1]):
        if j not in a:
            candidates.append(j)
    for j in candidates:
        a.append(j)
        sols=paths(G,u,v,a,sols)
        a.remove(j)
    return sols

pathsuv=paths(G,0,6)
# pathsuv.sort(key=lambda x:len(x))
for path in pathsuv:
    print(path)
    
nx.draw(G,with_labels=True)

[0, 1, 2, 3, 4, 9, 6]
[0, 1, 2, 3, 4, 9, 7, 5, 8, 6]
[0, 1, 2, 3, 8, 5, 7, 9, 6]
[0, 1, 2, 3, 8, 6]
[0, 1, 2, 7, 5, 8, 3, 4, 9, 6]
[0, 1, 2, 7, 5, 8, 6]
[0, 1, 2, 7, 9, 4, 3, 8, 6]
[0, 1, 2, 7, 9, 6]
[0, 1, 6]
[0, 4, 3, 2, 1, 6]
[0, 4, 3, 2, 7, 5, 8, 6]
[0, 4, 3, 2, 7, 9, 6]
[0, 4, 3, 8, 5, 7, 2, 1, 6]
[0, 4, 3, 8, 5, 7, 9, 6]
[0, 4, 3, 8, 6]
[0, 4, 9, 6]
[0, 4, 9, 7, 2, 1, 6]
[0, 4, 9, 7, 2, 3, 8, 6]
[0, 4, 9, 7, 5, 8, 3, 2, 1, 6]
[0, 4, 9, 7, 5, 8, 6]
[0, 5, 7, 2, 1, 6]
[0, 5, 7, 2, 3, 4, 9, 6]
[0, 5, 7, 2, 3, 8, 6]
[0, 5, 7, 9, 4, 3, 2, 1, 6]
[0, 5, 7, 9, 4, 3, 8, 6]
[0, 5, 7, 9, 6]
[0, 5, 8, 3, 2, 1, 6]
[0, 5, 8, 3, 2, 7, 9, 6]
[0, 5, 8, 3, 4, 9, 6]
[0, 5, 8, 3, 4, 9, 7, 2, 1, 6]
[0, 5, 8, 6]

Generar coloraciones de gráficas

También podemos hacer backtrack para encontrar coloraciones con cierto número de colores para una gráfica, si es que existen. Vamos avanzando en llenar un vector \((c_1,\ldots,c_k)\) con los colores correspondientes a los vértices \(v_1,\ldots,v_k\).

import matplotlib.pyplot as plt
G=nx.petersen_graph()
print(nx.nodes(G))
print(nx.edges(G))
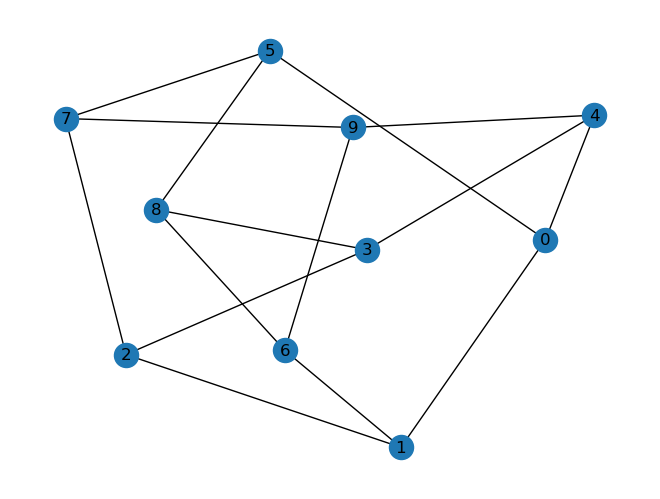
nx.draw_kamada_kawai(G,with_labels=True)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[(0, 1), (0, 4), (0, 5), (1, 2), (1, 6), (2, 3), (2, 7), (3, 4), (3, 8), (4, 9), (5, 7), (5, 8), (6, 8), (6, 9), (7, 9)]

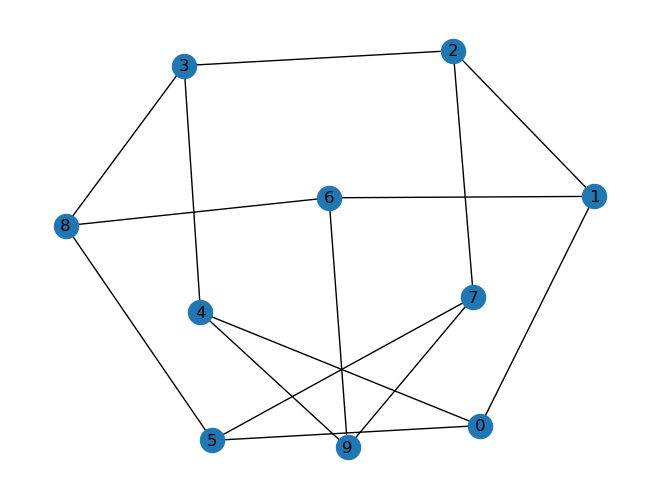
En este ejemplo buscamos coloraciones con tres colores.

En un inicio, los vértices no tienen asignados ningún color. Armamos el vector de una coloración asignando un color a un primer vértice y luego coloreando a cada otro vértice con un color que no haya sido ocupado por uno de sus vecinos. Repetimos esto hasta colorear todos los vértices, momento en que tendremos una solución válida.

def three_col(G,n,a=[],sols=[]):
    k=len(a)
    if k==n:
        sols.append(a.copy())
        return(sols)
    candidates=[0,1,2]
    for j in nx.all_neighbors(G,k):
        if j<k and (a[j] in candidates):
            candidates.remove(a[j])
    for j in candidates:
        a.append(j)
        sols=three_col(G,n,a,sols)
        a.pop()
    return(sols)

proper=three_col(G,10)
colors=['red','green','blue']

fig, axs = plt.subplots(3,3)
fig.set_figheight(15)
fig.set_figwidth(15)
print(len(proper))
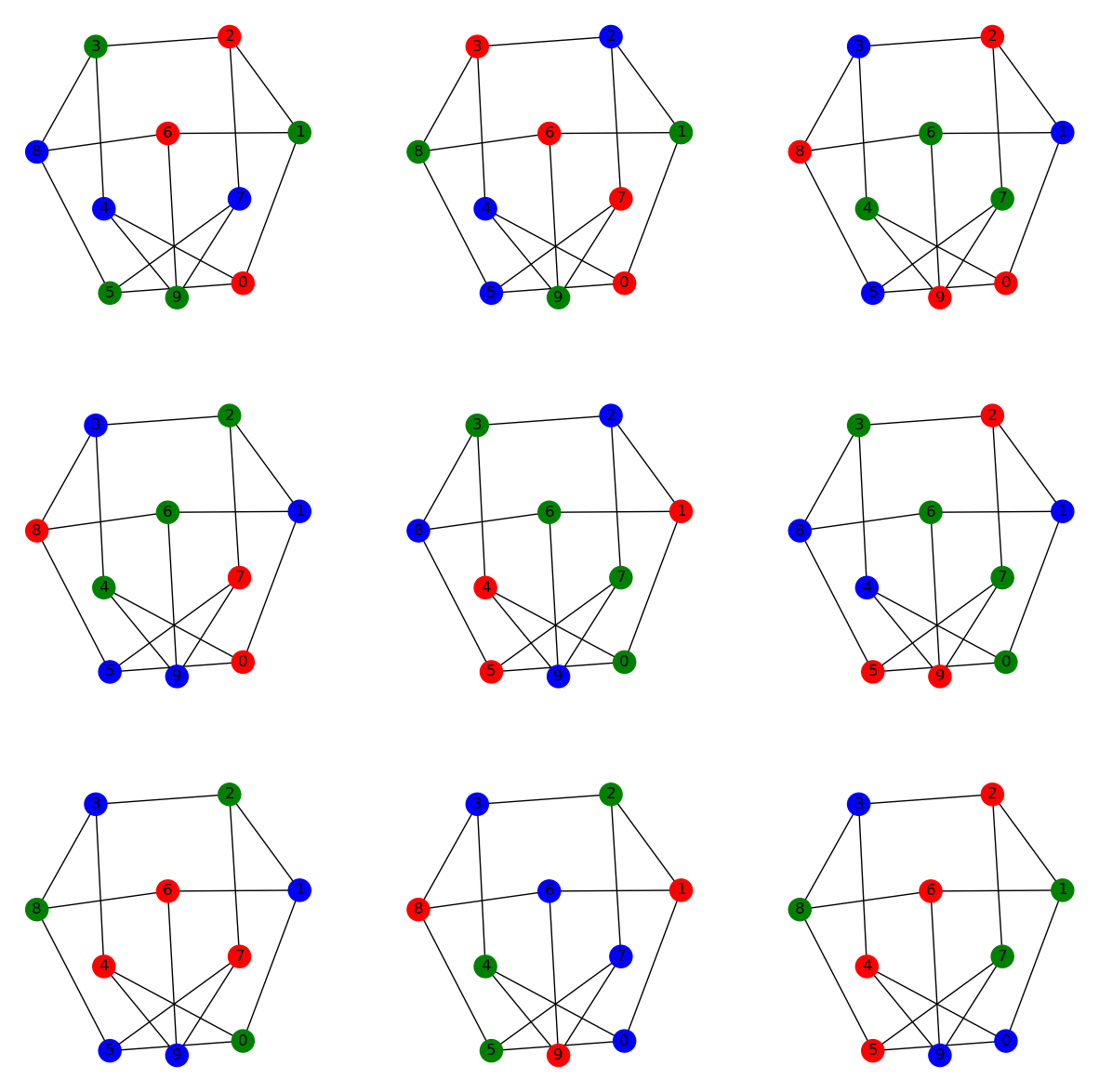
for k in range(9):
    one_proper=[colors[j] for j in proper[13*k]]
    nx.draw_kamada_kawai(G,node_color=one_proper,with_labels=True,ax=axs[int(k/3),k%3])

120

Intentemos ver el backtrack en acción.

Esta versión de la función para encontrar las coloraciones incluye las coloraciones «incompletas». Los vértices de color negro son aquellos que no tienen color asignado para dicha parte del algoritmo.

def three_col_accion(G,n,a=[],track=[]):
    k=len(a)
    track.append(a.copy())
    if k==n:
        return track
    candidates=[0,1,2]
    for j in list(nx.all_neighbors(G,k)):
        if j<=k and (a[j] in candidates):
            candidates.remove(a[j])
    for j in candidates:
        a.append(j)
        track=three_col_accion(G,n,a)
        a.pop()
    return track

proper=three_col_accion(G,10)

# Primer forma de dibujarlo
for k in proper:
    while len(k)<10:
        k.append(3)
print(len(proper))
colors=['red','green','blue','black']
j=0
plt.figure(figsize=(7,7))
for coloring in proper:
    plt.clf()
    nx.draw_kamada_kawai(G,node_color=[colors[k] for k in coloring],with_labels=True,node_size=1800,font_size=36)
    plt.savefig('backtrack/{:0>3}.png'.format(j))
    j+=1

120

# Segunda forma de dibujarlo
for k in proper:
    while len(k)<10:
        k.append(3)
print(len(proper))
colors=['red','green','blue','black']
j=0
plt.figure(figsize=(5,5))
for coloring in proper:
    plt.clf()
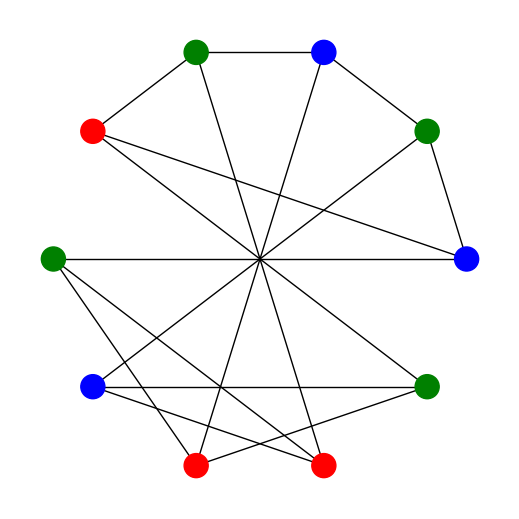
    nx.draw_circular(G,node_color=[colors[k] for k in coloring])
    plt.savefig('backtrack/c{:0>3}.png'.format(j))
    j+=1

120

Tarea moral

Los siguientes problemas te ayudarán a practicar lo visto en esta entrada. Para resolverlos, necesitarás usar herramientas matemáticas, computacionales o ambas.

1. Problema

2. Problema

3. Problema

4. Problema

5. Problema